Here we will learn about inequalities on a number line including how to represent inequalities on a number line, interpret inequalities from a number line and list integer values from an inequality.
There are also inequalities on a number line worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
Inequalities on a number line allow us to visualise the values that are represented by an inequality.
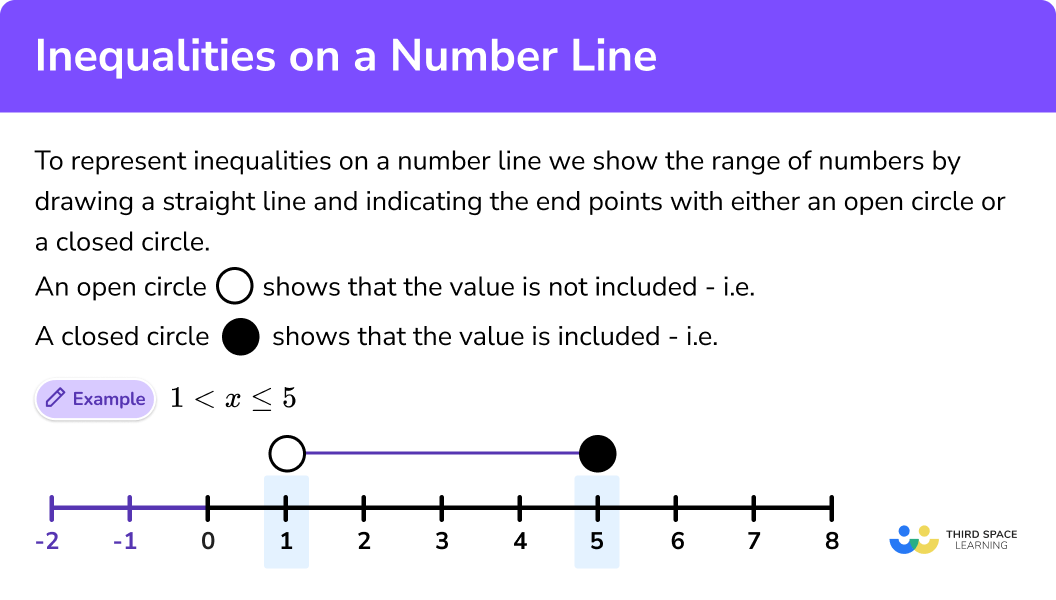
To represent inequalities on a number line we show the range of numbers by drawing a straight line and indicating the end points with either an open circle or a closed circle.
An open circle shows it does not include the value.
A closed circle shows it does include the value.
The solution set of these numbers are all the real numbers between 1 and 5 .
As 1 has an open circle, it does not include ‘ 1 ’ but does include anything higher, up to and including 5 as this end point is indicated with a closed circle.
We can represent this using the inequality 1 < x \leq5
We can also state the integer values (whole numbers) represented by an inequality.
In this example, the integers 2, 3, 4 and 5 are all greater than 1 but less than or equal to 5 .
The solution set can represent all the real numbers shown within the range and these values can also be negative numbers.

In order to represent inequalities on a number line:
An open circle needs to be indicated at ‘ 3 ’ on the number line.
Represent 2\leq on a number line.
An open circle needs to be indicated above ‘ 2 ’ and a closed circle needs to be indicated above ‘ 6 ’.
Then draw a line between the circles to indicate any value between these circles.


Get your free Inequalities on a number line worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free Inequalities on a number line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Inequalities on a number line is part of our series of lessons to support revision on inequalities. You may find it helpful to start with the main inequalities lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Represent x > 3 on a number line.
In this example it is 3 .
2 Decide if this needs to be indicated with an open circle or a closed circle.
As the symbol is > then it will be an open circle.
3 Decide if the straight line needs to be drawn to the right or the left of the circle.
As x is greater than 3 the straight line needs to be drawn to the right hand side of the circle to show the solution set of values greater than 3 .
Represent −2\geq on a number line.
Identify the value that needs to be on the number line.
In this example it is −2 .
Decide if this needs to be indicated with an open circle or a closed circle.
As the symbol is \geq then it will be a closed circle.
Decide if the straight line needs to be drawn to the right or the left of the circle.
As x is less than or equal to −2 the straight line needs to be drawn to the left hand side of the circle to show the solution set of values less than −2 .
Represent 2\leq\leq on a number line.
Identify the values that need to be indicated on the number line.
In this example they are 2 and 7 .
Decide if they need to be indicated with open circles or closed circles.
As the symbols are both there will be two closed circles.
Draw a straight line between the circles to represent the solution set.
Represent −2\leq on a number line.
Identify the values that need to be indicated on the number line.
In this example they are −2 and 3 .
Decide if they need to be indicated with open circles or closed circles.
Draw a straight line between the circles to represent the solution set.
Write the inequality that is shown on this number line.
Identify the value indicated.
In this example it is ‘ 4 ’.
Decide which inequality symbol to use.
As the circle is closed and the values indicated are greater than 4 we use the inequality is x\geq
Write the inequality that is shown on this number line:
Identify the values indicated on the number line.
In this example they are −2 and 4 .
Decide which inequality symbol to use.
As the circle above the −2 closed we include the −2 and use -2\leq.
As the circle above the 4 is open we do not include the 4 and use x < 4 .
Put the inequalities together.
List the integer values satisfied by the inequality -4\leq
Identify the values indicated on the number line.
In this example they are −4 and 2 .
−4 is included as it is followed by \leq
2 is not included as < is before it.
List the integer values.
List the integer values satisfied by the inequality shown on the number line below.
Identify the values indicated on the number line.
In this example they are -2 and 4 .
−2 is not included as it is represented by an open circle.
4 is included as it is represented by a closed circle.
List the integer values.
A common error is to confuse open circles and closed circles:
Open circles do not include the value so require a ‘Closed circles do include the value so require a ‘\leq'
A common error is to not recognise the symmetry about ‘0’ on the number line, and therefore not comparing the size of negative numbers correctly.
E.g.
5 is greater than one as they are ordered 1 , 2, 3, 4, 5 on a number line.
But −5 is less than −1 as they are ordered −5 , −4, −3, −2, −1 , 0, 1, 2, 3 on a number line.
The direction of the inequality sign shows if the solution set is ‘greater than’ or ‘less than’. This can be confused when both sides of the inequality are switched. For example x > 8 is the same as 8 < x and ‘x’ is greater than 8 as the inequality sign is open towards the ‘x’ .
Usually integer values are requested to be listed in a solution set. ‘0’ can sometimes be forgotten.